
A mole in chemistry is just a group word for an amount of mass you want to use in a chemical reaction. Essentially, a mole is a standard unit of measurement that represents $\small 6.022\:\times \:10^{23}$ particles (atoms, molecules, ions, or the like). That is 602 hexillion particles. While this seems like an incomprehensibly large number, atoms are so small that this is really less than a cup of solid or liquid material. How would you know how many particles (atoms, molecules, ions…) you had in a scoop of solid or liquid substances? You certainly can’t count that high. A carpenter might feel the same way when buying nails for a project—the store usually weighs them rather than counting them individually. Chemists use mass to determine the number of particles in a chemical reaction; the term for this large number of atoms chemists use is known as Avogadro’s number.
Every great chemist knows the value of grasping the fundamental concept of the mole. In a world where chemical reactions are followed meticulously on a delicate scale, a thorough understanding of Avogadro's number and its mathematical equivalent is essential for predicting the outcome of reactions and determining the unknown amounts produced within a reaction.
Table of Contents:
- What Is a Mole in Chemistry?
- How Is a Mole Calculated?
- The Importance of the Mole Concept in Chemistry
- The History and Origin of the Mole
- Examples of Mole Calculations
- Conclusion
What Is a Mole in Chemistry?
The mole is a staple of chemistry, but what does it really mean? In essence, a mole is a fundamental amount of any substance. It is defined as the amount of substance that contains the same number of atoms, molecules, or ions as there are in 12 grams of carbon-12. As researchers determined there to be $\small 6.022\:\times \:10^{23}$ atoms in 12 grams of carbon-12, this value became the standard number of particles for any one mole of that substance, and it is defined as Avogadro's number.
The mole allows chemists to convert between the mass of a substance and the number of particles it contains, facilitating calculations in chemical reactions and stoichiometry. By using moles, chemists can express concentrations, perform dilution calculations, and determine yields, making it an essential concept in both theoretical and practical chemistry.
Definition of a Mole, Avogadro's Number, Molar Mass, Atomic Mass, and Molecular Weight
A mole is the International System of Units (SI) base unit used to measure how many atoms or molecules are used in a reaction. To reiterate, one mole is defined as the quantity of any chemical substance that contains as many particles (atoms or molecules) as there are atoms in 12 grams of carbon-12, or 602 hexillion particles.
The number of elementary entities in one mole of any substance is known as Avogadro's number of that substance. It is named after the Italian scientist Amedeo Avogadro. Through years of experimentation, this value has been determined to be approximately 6.02214076 × 10²³.
Molar mass and atomic mass can often be confused with one another; molar mass is the mass of one mole of a particular element, expressed in grams per mole (g/mol). Atomic mass refers to the mass of a single atom of an element, typically measured in atomic mass units (amu). An atomic mass unit is 1/12 the mass of a carbon 12 atom; you can think of it as close to the mass of a proton or neutron. The two terms are related in that the molar mass (in grams per mole) is equivalent to all elements’ atomic mass (in amu) shown in the formula in grams. So, for water, the atomic mass for 2 hydrogen atoms and 1 oxygen atom is roughly 18 AMU. The molar mass of water would be 18 grams.
Teaching Tools
Mole Set
Visualize one mole of copper, iron, zinc, and aluminum with the Mole Set! Use the set to practice distinguishing specimens by density, atomic mass, specific heat, and more.Knowing a substance’s atomic mass helps determine how many atoms are present in a given sample. For instance, by dividing the total mass of a substance, measured on a scale, by its atomic mass, one can calculate the number of atoms in that sample. The new number you calculate will have the unit of atoms, ions, or particles.
Further, let’s define molecular weight (MW), as it can also need clarification. Molecular weight and molar mass are closely related but not exactly the same. Molar mass, as defined above, refers to the mass of one mole of a substance, expressed in grams per mole (g/mol), and is numerically equivalent to the molecular weight but differs in units. Molecular weight, on the other hand, is the weighted average mass of the atoms in a molecule based on the relative abundances of its isotopes, typically expressed in atomic mass units (amu). While the numerical values are the same for a given substance, molar mass is used for the macroscopic measurements used in chemistry, whereas molecular weight is often used when talking about the size of molecules or formula units.
How Is a Mole Calculated?
Understanding how to calculate the mole is essential in chemistry, as it allows scientists to relate the mass of a substance to the number of particles it contains, facilitating accurate measurements and calculations in various chemical processes.

Calculating Moles Using Mass, Chemical Equations, and Conversions
To calculate the number of moles of a substance, you need to know its mass (typically measured in grams) and its molar mass. The molar mass is the sum of the masses of each atom in the formula unit for ionic compounds or the molecular formula for covalent compounds. Once you have these values, simply divide the mass of your sample by the molar mass.
Example: Find the number of molecules of 15 grams of $CO_2$ which has a MW of 44.01 (12.01+16.00+16.00=44.01).
15g of $CO_2$ contains $ \large {\frac {15} {44.01} }$ = 0.32 mol of $CO_2$
Chemical equations represent the relative amounts of reactants and products in a reaction. The coefficients in a balanced equation indicate the mole ratios of each substance. We can use these ratios to calculate the moles of any substance in the reaction if we know at least the number of moles of one other substance. For example, if you start with 0.32 moles of $CO_2$.
$2CH_4 + 3O_2 \rightarrow 2CO_2 + 4 H_2O $
0.32 mol $CO_2 \times \large{\left ( \frac {4\;mol\;H_2O}{2\;mol\;CO_2} \right )}$ = 0.64 mol of $H_2O$
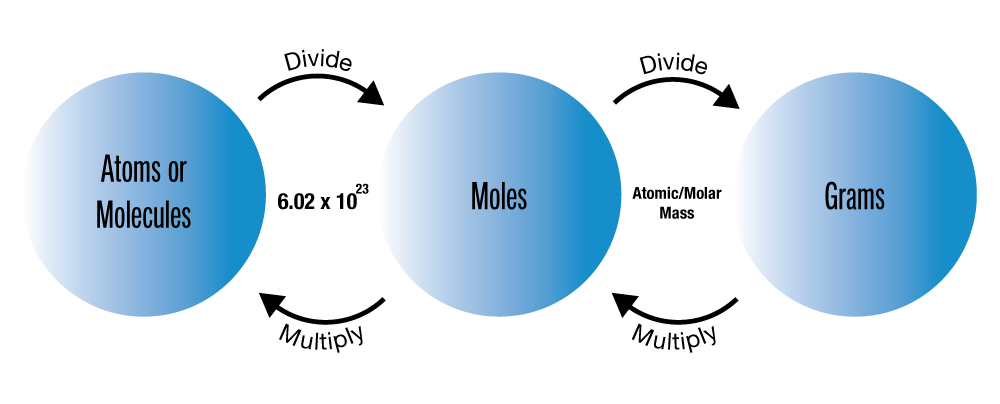
It's not just about the numbers; converting between moles, mass, and particles is the thread that weaves together many of the fundamental concepts in chemistry. Mastering these conversions is essential for accurately solving problems in stoichiometry and thermodynamics.
The Importance of the Mole Concept in Chemistry
The mole concept is a cornerstone of chemistry, providing a standardized method for quantifying substances that enables scientists to understand and predict the behavior of matter in chemical reactions and interactions. So far we’ve stated:
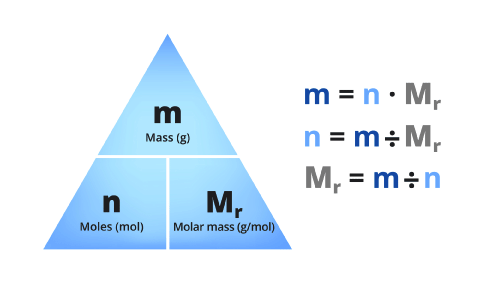
mass = number moles x Molecular Weight
which can be represented as:
m = n x MW
Some texts show this triangle to relate the three:
Other texts describe it this way:
Simplifying Complex Calculations, A Mole in Stoichiometry, and A Mole in Everyday Life
Using moles allows us to transform complex chemical reactions into digestible data. This conversion of atomic mass to molar mass turns calculations like stoichiometry and thermodynamics from intimidating lab reports into conquerable tasks.
The advantage of using molar mass over molecular weight lies in its practical application for calculations in chemistry. Molar mass, expressed in grams per mole (g/mol), allows chemists to directly relate the mass read off a scale of a substance in a laboratory setting to the number of moles, which in turn corresponds to the number of particles or entities (atoms, molecules, etc.).
The conversion to molar mass makes it easier to perform stoichiometric calculations, prepare solutions, and conduct reactions, as it provides a straightforward way to measure and quantify substances on a macroscopic scale, while molecular mass is typically used for understanding individual atoms, molecules, or formula units and their properties.
The mole concept has numerous practical applications in our daily lives. Pharmaceutical companies use moles to precisely measure the active ingredients in medications, environmental scientists use moles to quantify pollutant concentrations, and chemical engineers use moles to design and optimize industrial processes.

The History and Origin of the Mole
The concept of the mole has its roots in the development of atomic theory and the need for a systematic way to quantify chemical substances. The term "mole" was first introduced in 1896 by the German chemist Wilhelm Ostwald, who derived it from the Latin word "moles," meaning "mass" or "bulk." However, the idea of relating the mass of a substance to the number of particles it contains can be traced back to early 19th-century chemists like John Dalton, who proposed atomic theory, and Amedeo Avogadro, who formulated Avogadro's law in 1811. Avogadro's work established that equal volumes of gases at the same temperature and pressure contain an equal number of molecules, leading to the realization that a mole corresponds to a specific number of entities—later defined as Avogadro's number. The mole was officially adopted as a standard unit in the International System of Units (SI) in the 1970s, solidifying its importance in modern chemistry for facilitating calculations involving the amounts of substances in chemical reactions.
Amedeo Avogadro's Contribution, Adoption as an SI Unit
The mole story begins before the term “mole” was even coined, with Amedeo Avogadro. Amedeo Avogadro was an Italian scientist born on August 9, 1776, in Turin, Italy, and he made significant contributions to the field of chemistry, particularly during the early 19th century. He is best known for Avogadro's law, formulated in 1811, which states that equal volumes of gases contain an equal number of molecules (as stated in the previous paragraph) regardless of the type of gas. This groundbreaking insight challenged the prevailing views of the time, which often conflated the properties of gases with their weights.
Avogadro's work laid the foundation for the concept of the mole, leading to the development of the idea that a specific number of particles—later defined as Avogadro's number or Avogadro’s constant ($\small 6.022\:\times \:10^{23}$)—exists in one mole of any substance. Although his contributions were not fully recognized during his lifetime, Avogadro's theories ultimately revolutionized the understanding of molecular theory and stoichiometry in chemistry, making him a pivotal figure in the scientific community.

The mole was officially adopted as a standard unit in the International System of Units (SI) in 1971, during the 14th General Conference on Weights and Measures (CGPM). This conference recognized the mole as one of the seven base units in the SI system, allowing it to serve as the universal unit for quantifying the amount of substance in chemical contexts. Prior to this formal recognition, the concept of the mole was already in use among chemists, particularly in relation to Avogadro's work, but its establishment as an official unit provided a standardized framework for scientific communication and calculations in pure and applied chemistry.
Examples of Mole Calculations
We're going to get hands-on with mole calculations by tackling a few relevant examples. As we walk through these scenarios, the mole concept will start to make more sense in the context of real-world applications.
Mole Calculation for Water, Mole Calculation for Carbon Dioxide, Mole Calculation for Glucose
Let's calculate the number of water molecules in a sample of water with a mass of 36.04 grams. First, we calculate the number of moles of water, then multiply by Avogadro's number to get 1.20 × 1024 water molecules.
$ \text{Given amount} \;\;\rightarrow\;\; \text{moles} \;\;\rightarrow\;\; \text{molecules} $
$ \text{36g}\:H_2O \left( \large \frac {1\:mol\:H_2O} {18g\:H_2O} \right) \left( \large \frac {6.02\:\times \:10^{23}\;H_2O} {1\:mol\:H_2O} \right )\:\text {= ________ molecules of} \: H_2O $
$ \text{Or} $
$ \text{36g}\:H_2O\:\div\:\text{MW}\:H_2O\; \times \;6.02\:\times \:10^{23}\:\text {= ________ molecules of} \: H_2O $
Consider a sample of carbon dioxide ($CO_2$) with a mass of 44 grams. Each mole of $CO_2$ contains one mole of carbon atoms, so the 44-gram sample contains approximately 6.02 × 1023 carbon atoms.
$ \text{Given amount} \;\;\rightarrow\;\; \text{moles of}\:CO_2 \;\;\rightarrow\;\; \text{molecules of}\:CO_2 \;\;\rightarrow\;\; \text{atoms of} \; C $
$ \text{44g}\:CO_2 \left( \large \frac {1\:mol\:CO_2} {48g\:CO_2} \right) \left( \large \frac {6.02\:\times \:10^{23}\;CO_2} {1\:mol\:CO_2} \right ) \left( \large \frac {1\;\text{atom C}} {1\;\text{molecule}\;CO_2} \right )\:\text {= ________ atoms of} \; C $
$ \text{Or} $
$ \text{44g}\:CO_2\:\div\: \text{MW}\:CO_2 \;\times \;6.02\:\times \:10^{23}\: \times \: \text{1 atom of C per}\: CO_2 \: \text {= ________ atoms of} \: C $
Glucose ($C_6H_{12}O_6$) is a simple sugar and a key energy source for living organisms. To calculate the mass of glucose that contains 3.01 × 1023 molecules, we first convert molecules of glucose to moles, then calculate the mass using the molar mass. The result is 90.08 grams of glucose.
$ \text{Given amount} \;\;\rightarrow\;\; \text{moles of}\:C_6H_{12}O_6 \;\;\rightarrow\;\; \text{grams of}\:C_6H_{12}O_6 $
$ 3.01\:\times \:10^{23}\: C_6H_{12}O_6\: \left( \large \frac {1\:mol \: C_6H_{12}O_6} {6.02\:\times \:10^{23}\:C_6H_{12}O_6} \right) \left( \large \frac {180g\:C_6H_{12}O_6} {1\:mol\:C_6H_{12}O_6} \right )\;\text {= ________ grams of }\: C_6H_{12}O_6 $
$ \text{Or} $
$ 3.01\:\times \:10^{23}\;C_6H_{12}O_6\:\div\:6.02\:\times \:10^{23}\:C_6H_{12}O_6\:\times \; 180g\:\text{per mol}\:C_6H_{12}O_6 \: \text {= ________ grams of }\: C_6H_{12}O_6 $
In the lab, imagine moles as a trusted measuring cup, precisely quantifying the amount of a substance. Calculate moles using mass, chemical equations, and conversions to master the art of measuring substances involved in chemical reactions.
Conclusion
Chemical equilibrium is a cornerstone of chemistry that helps us understand the behavior of chemical reactions. It's a state of balance where the forward and reverse reactions proceed at equal rates, resulting in no net change in the concentrations of reactants and products. The equilibrium constant defines the ratio of the equilibrium concentrations of products to reactants (with each concentration raised to the power of its stoichiometric coefficient), thereby determining the position of equilibrium in a chemical reaction. This balance is crucial, as it helps us comprehend the intricate relationships between chemical reactions and their equilibrium states.


